图片模型
模糊图B、潜在图L与模糊核K的关系为:
其中,⊗代表卷积(非周期边界条件),N表示每个像素上的传感器噪声。
我们假设图像的像素值与传感器的辐照度线性相关。潜在图像L代表我们的目标图像;我们的目标是从B中恢复L,而没有对K的具体知识。
自然图像在梯度上满足重尾分布。下图显示了一幅自然图像及其梯度大小的直方图。分布表明,图像主要包含小的或零的梯度,但少数梯度有较大的幅度。我们用零均值高斯混合模型表示梯度的分布。之所以选择这种表示方式,是因为它可以很好地逼近经验分布,同时允许对我们的算法进行易于处理的估计。
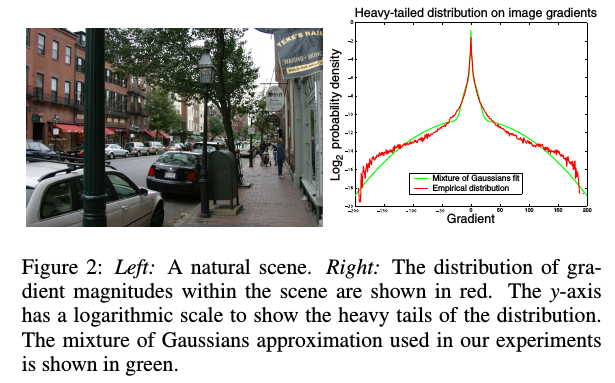
重尾分布:梯度分布大多集中在小值上,但比高斯分布更有可能取到大值。这与直觉相对应,图像大面积存在恒定强度或柔和强度,因此梯度整体变化不大,偶尔会出现边缘或边界上因遮挡发生的大变化。
算法
总体框架
第一步:从输入的图片中得到模糊核,估计过程是以粗到细的方式进行,以避免局部最小值。
第二步:利用估计核函数,应用标准卷积算法估计潜在的(Unblurred)图像。
算法输入
- 模糊图像B
- 模糊图像中的一个方块
- 模糊核大小上的上界(以像素为单位)
- 关于模糊核(水平或垂直)方向的初始猜测
预处理过程
我们要求输入图像B在处理之前已经转换成线性颜色空间。在实验中,我们应用了$\gamma=2.2$的逆伽玛校正。
1
2
3
4
5
6if (GAMMA_CORRECTION~=1)
%%% gamma correct actual image
obs_im = (double(obs_im).^(GAMMA_CORRECTION))/(256^(GAMMA_CORRECTION-1));
else
obs_im = double(obs_im);
end为了估计预期的模糊内核,我们将原始图像的所有颜色通道合并到用户指定的块中,生成灰度模糊块P
模糊核的求法
在给定灰度模糊块P时,我们以L的统计数据作为先验为指导,通过寻找概率最高的值来估计K和潜在的块图像$L_p$。因为先验知识是在梯度上而非亮度,因此选择梯度进行优化。卷积是线性操作,因此可以使用
这里假设噪声满足方差为$\sigma^2$的高斯分布。
潜在图像的梯度$p(\nabla L_p)$是一个混合的C-零均值的高斯混合分布,即满足第C个高斯满足方差为$v_c$权重为$π_c$;我们对内核使用一个稀疏先验$p(K)$,它鼓励内核中的零值,并且要求所有条目都是正的。具体来说,核值的先验是混合D指数分布,即对于第d个构成,比例因子为$\lambda_d$,权重因子为$\pi_d$。
在$\nabla P$已知的情况下(可以统计测量得到),通过贝叶斯公式,可以得到后验概率:
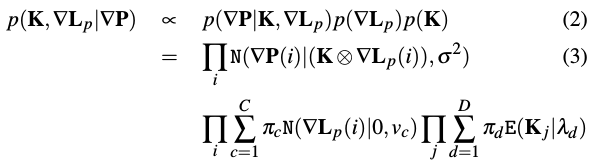
其中,$i$代表图像中的像素点,而$j$代表模糊核的;N和E分别代表高斯和指数分布。便于处理,假设$\nabla P$彼此之间相互独立,像$\nabla L_p$与$K$一样。
该问题的直接解决方法是将其视为一个最大后验概率问题,即求核$K$与潜在图像的梯度$\nabla L$使得$p(K,\nabla L_p|\nabla p)$最大。这相当于解决一个正则化的最小二乘问题,试图拟合数据,同时也使小梯度最小化。该方法行不通。
取而代之,使用近似后验分布$p(K,\nabla L_p|\nabla p)$,用最大边际概率计算核$K$。该方法选择最可能与潜在图像的分布有关的核,从而避免了在选择图像的单个“最佳”估计时可能发生的过拟合。
为了更好的计算这个近似,这里使用了变分贝叶斯的方法,使用$q(K,\nabla L_p)$去代替$p(K,\nabla L_p|\nabla p)$。且满足因式分解$q(K,\nabla L_p)=q(K)q(\nabla L_p)$。对于潜在的图像梯度,这种近似是高斯密度,而对于非负模糊核元素,这种近似是一种经矫正的高斯分布。每个潜在图像的梯度和模糊核元素的分布由它们的均值和方差表示,并存储在一个数组中。此外,我们的方法基于Miskin and MacKay对动画图像进行盲反卷积的方法。
根据Miskin and MacKay,在评估过程中,将噪声变量$\sigma^2$视为一个未知量,可以将用户从调优过程中解放出来。这允许噪声方差在估计过程中发生变化:数据拟合约束在过程的早期是松散的,随着找到更好的、低噪声的解决方案,数据拟合约束变得更紧。设$\sigma^2$在逆方差上有gamma分布,有超参数a,b,$p(\sigma^2|a,b)=\Gamma(\sigma^2|a,b)$。$\sigma^2$的变分后是$q(\sigma^2)$,另外一个gamma分布。
变分算法的最小化的是模拟分布与真实分布之间的距离。即:$KL(K,\nabla L_p,\sigma^2||p(K,\nabla L_p|\nabla p))$。变分后验中的独立性假设允许对成本函数$C_{KL}$进行因式分解:

其中$<\cdot>_{q(\theta)}$ 代表$q(\theta)^2$。为简便起见,依赖$∇p$省略了。
$q(K)$与$q(\nabla L_p)$分布的均值设置为$K$与$\nabla L_p$,分布的方差较高,反映了初始估计的不确定性。然后通过坐标下降交替更新分布参数;其中一个是通过在合并模型先验的同时将另一个边缘化来更新的。更新是通过计算封闭形式的最优参数更新,并在这些更新值的方向上执行行搜索(详见附录A)。一直更新直到$KL$可以被忽略。边缘分布$
在上面概述的公式中,我们忽略了图像中饱和像素的可能性,这是一种尴尬的非线性,违背了我们的模型。由于显式地处理它们比较复杂,所以在推理过程中我们更喜欢简单地掩盖图像的饱和区域,这样就不会用到它们。
在变分框架中,在$K$与$\nabla L_p$的先验使用了C=D=4个元件。潜在图像中方差$v_c$权重$π_c$使用EM通过街景图像估计得到。由于图像统计量随尺度而异,每个尺度级别都有自己的一组先验参数。这个先验被用于所有的实验。模糊核元素的先验参数是由一组从真实图像中推断出来的低噪声核估计出来的。
多尺度方法
上一节描述的算法受局部极小值的影响,特别是对于大的模糊核。因此,我们通过从粗到精的方式改变图像分辨率来进行估计。在粗级别,K是3x3的核。以确保正确的算法,我们手动指定初始3×3模糊内核两种简单的模式。然后,在保持K固定的情况下,运行推理方案,得到潜在梯度图像的初始估计。
然后我们回到金字塔,在每一层运行推理;$K$与$\nabla L_p$的聚合值被上采样作为推理的一个初始化在未来扩大规模。在最好的尺度上,推理收敛到全分辨率的核K。
用户监督
虽然使用全梯度图像$∇L$运行多尺度推理方案似乎更自然,但在实践中,我们发现,如果手工选择具有丰富边缘结构的小块,该算法的性能更好。手动选择允许用户避免大面积的饱和或均匀性,这可能是干扰或无信息的算法。此外,该算法在一个小块上比在整个图像上运行要快得多。
另外一个参数是模糊内核的最大大小。在图像中遇到的模糊的大小差别很大,从几个像素到几百个像素不等。如果算法是用一个非常大的内核初始化的,那么很难解决小的模糊问题。相反,如果使用的内核太小,就会出现大的模糊。因此,对于所有条件下的操作,内核的大约大小是用户所需的输入。通过检查图像中的任何模糊伪影,可以很容易地推断出内核的大小。
最后,我们还要求用户在模糊内核的两种初始估计中选择一种:水平线或垂直。尽管算法通常可以在任何一种状态下初始化,并且仍然生成正确的高分辨率内核,但这确保了算法开始在正确的方向上搜索。通过查看图像中任何模糊的内核工件,可以很容易地确定适当的初始化。
图像重建
$L$通常很大,考虑到速度,简单的方法很有吸引力,因此,我们用RL重建了潜在的彩色图像$L$。虽然RL方法的性能与其他评价方法相当,但它的优点是只需几分钟,即使是在大图像上(其他更复杂的方法,需要数小时或数天)。RL是一种非盲反卷积算法,它迭代最大化泊松统计图像噪声模型的似然函数。与更直接的方法相比,这种方法的一个好处是,它只提供非负的输出值。我们利用Matlab的实现算法来估计$L$,给定$K$,对每个颜色通道进行独立处理。我们使用了10次RL迭代,尽管对于大的模糊内核,可能需要更多。在运行RL之前,我们根据内核中的最大强度值,通过应用动态阈值来清除$K$,该阈值将某个值以下的所有元素设置为零,从而降低内核噪声。然后使用$γ=2.2$对RL的输出进行$γ$校正,并将其灰度直方图与$B$的灰度直方图(使用matlab的histeq函数)进行匹配,从而生成$L$。
附录


点评
在图像去模糊之初探—Single Image Motion Deblurring文章中,作者给出了这样的点评:
以往的芒去卷积方法要么对卷积核有很强的先验假设,要么对图像有一定的先验假设,或者两者都有。而且,这些方法往往不大适合较大的模糊核。Fergus等提出的方法完全抛弃了这些束缚, 实现了真正意义上的实用的BID。在此文中,图像去模糊主要被划分成了两步:卷积核的估计和去模糊。其中去模糊可以采用任何一种现有的算法,因此此文的重点集中在了模糊核的估计上。基于对图像模型统计特性的分析,此文深入研究了模糊图像和非模糊图像的梯度分布,提出了一种基于梯度分布模型的去模糊算法。自然的清晰的图像满足特定的heavy-tailed distribution,而模糊图像的梯度分布则想去甚远。因此Fergus等基于这种特性构造了在已知观测图像情况下原始图像和模糊核的联合后验概率,后验概率最大化对应的原始图像和卷积核的组合就是所要的答案。然而直接解这个MAP(Maximum a Posterior)问题,却得不到正确的答案。因此作者采用了一种学习的方法,即MISKIN和MACKAY,在Ensemble Learning for Blind Image Separation and Deconvolution中提到的方法。这也是作者认为的两大贡献。
Fergus在paper和ppt中都给出了一些结果,其实结果都不能完全令人满意,有的恢复的效果不够好,有的噪声实在太大。但作者也说他的paper有不少可改进的地方,言外之意就是此文只是提出了一种思想,效果有待完善。这也让本文留下了不少可研究的空间,个人认为有以下三个方面可以改进:(1)图像模型的选择。梯度模型只是选取了相邻的两个点的统计特性,有点过于简单。清晰图像有很大可能满足作者采用的heavy-tailed distribution,但满足这种分布的一定是效果比较好的清晰图像吗?Gibbs效应如何克服?此文并没有深入研究 (2)MAP算法的优化 (3)本文采用的R-L这个经典古老的算法,肯定有其他更好的算法能改善图像质量。
MATLAB代码
- 首先读入图片,obs_im。
- 然后经过提取单通道或者grayscale得到单通道的图,其中grayscale操作将大于250的像素值均变为了255。obs_im_orig为原obs_im。
- 将obs_im与obs_im_orig,事前resize,变为之前的1/2,使用的是bilinear插值法。
- 对obs_im经过gamma校正
- 强度变换
- 额外的模糊高斯变换(始终没有起作用)
- 根据像素值大于250的视为饱和,产生mask
- 是否自动寻找patch(默认无作用)
- CAMERA_TYPE是否为“unknown”(默认均为“unknown”)
- 如果COLOR有值,则转换YIQ空间(默认无作用)
- 将obs_im与mask分别赋值给obs_im_all与mask_all
- 求图像的梯度。首先判断为harr算法或者laplace算子。进行卷积操作求出x与y方向上的卷积,接着组成整个梯度。
- 求$\nabla p^s$。根据事先给定的方块的位置,进行剪切。从obs_im_all中剪切出来指定的块赋值给obs_im,从mask_all中剪切出来特定的块赋值给mask。剪切出来x与y方向上的梯度分别赋值给obs_grad_x与obs_grad_y。判断条件跳入先梯度后恢复图像大小。求循环的scale梯度放置到数组obs_grad_scale_x与obs_grad_scale_y中,求循环的mask scale放置到mask_scale中。
- 将obs_grad_scale_x与obs_grad_scale_y按照s分别进行拼接放置到obs_grad_scale中。
- 求公式中的$K^s$,即求K的scale。由公式可得:$K^{s-1}=\frac{1}{\sqrt{2}}K^{s}$。$K^s$中的s等于1的时候,使用高斯在初始$K^9$进行卷积,然后resize。最终所有元素除以对应的最大值,完成归一化操作,赋值给blur_kernel_scale。
- 如果不是合成图像,则首先将obs_grad_scale赋值给obs_grad_scale_old;delta_kernel函数的作用是输入一个值,生成奇数(非奇数也要变成奇数)矩阵,矩阵中心的值为1。根据特定的s产生对应的db,根据fft2,ifft2产生新的obs_grad_scale与mask_scale。
- 统计$K^s$(blur_kernel_scale)的K(s)、L(s)、hK(s)与hL(s)。统计$\nabla p^s$(obs_grad_scale)的M(s)、N(s)。根据BLUR_COMPONENTS,$K(s)\ast L(s)$,产生全零矩阵spatial_image_mask。根据size(mask_scale{s})产生全零矩阵spatial_image_mask。如果FFT_MODE为真,则由M(s)、N(s)产生I(s)、J(s),产生全零矩阵Dp{s},接着产生D(s)。
- 进行主循环,首先将priors进行扩展。接着调用MISKIN和MACKAY的算法
- 运行RL重建算法,还原图像
参考资料
图像去模糊之初探—Single Image Motion Deblurring
Rob Fergus的Removing Camera Shake from a Single Photograph

